2019年1月の記事一覧

「美しい図形と奇妙な空間」
 
東京ジャーミイ（代々木上原，東京）にある装飾です．左写真は説教壇の横にあります．
複雑な図形ですが美しい．イスラムのデザインによく見られます．
右の写真はステンドグラスです．
これらの図形の美しさの原因は，図形の中が黄金比だらけだからのようです．

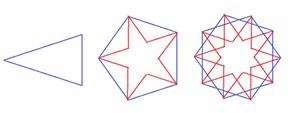
これらの図形の成り立ちを，以下の図で説明しましょう．
図の一番左は辺の長さが黄金比の2等辺三角形です．
つまり，底辺を１とすると，等しい２辺は1.618...
真ん中の図は，正5角形の中にできる星形で，星の頂角は黄金比の三角形にでてくる頂角36°と同じです．
一番右の図は，この星型とこの星型を180°回転したものを重ね合わせたものです．
東京ジャーミイの美しい図形は，星形を２つ重ね合わせたものになっているのにお気づきでしょうか．

 
星形を2つ重ねた図形の対称性はどのように記述しましょうか．
まず，星形の対称性は．点群5mです（５は5回回転対称軸，mは鏡映面）．
星形を重ねた図形には，2回回転対称軸２が生じ部分群として点群２も含まれます．
結局，2⊗5m＝10mmの点群になります．
あるいは，星形5mを「法」にすると，10回回転操作（36°の回転）の作る群は
｛１，10(mod5m)｝のような，位数2の点群として解釈することもできます．
この考え方の奇妙な所は，36°回転を2回続けると元の星形に重なるから振り出しに戻ったと見なすわけです．

我々の3次元ユークリッド空間では360°回転しないと元に戻らないのですが，この奇妙な空間にいたとすると
2x36°＝72°回転すると元に戻ることになります．

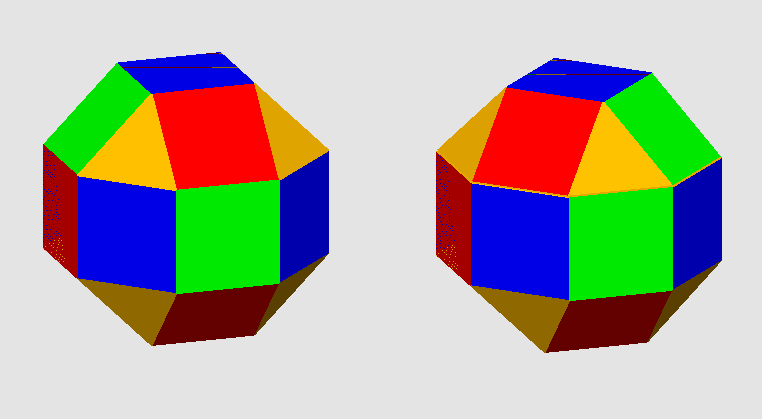
左の多面体は半正多面体［3,4,4,4］といいます［頂点に正3角形，正4角形，正4角形，正4角形が集まっていることを表示するシュレーフリの表記法です］．右はミラーの立体といいますが，シュレーフリの表記法では，半正多面体と同じになります．しかし，ミラーの立体は半正多面体に入れないのが慣例（入れても良いのにね）です．対称性でいうと左は正6面体や正8面体と同じ対称性ですが，右は4mmの対称性です．（図の作成はpov-ray使用による）