
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
壁紙模様の対称性は17種類の平面群に分類されます.17種類の平面群の表を説明に先立ち掲載しておきます.
この表には,国際記号とロシア式記号の2通りの平面群の記述法を併記したので比較できます.今日,国際記号が一辺倒に普及していますが,群の生成元が明示されるロシア式記号は,理論的視点では特に重要です.
両方の記号の仕組みを理解するのが,この節の目標です.
ここに表示される平行四辺形は2次元の単位胞で,水平方向の軸は$$b$$,上下方向の成分をもつ軸は$$a$$(3次元の場合;紙面に垂直な軸は$$c$$)とします.
有限図形の対称性を考えるとき,対称操作の不動点となる1点(特異点と呼ぶ)があります.例えば,正6角形の対称性を考えるとき,正6角形の中心がこの特異点で,この点を通過する回転対称軸が6回回転対称軸です.
次に,このような特異点(不動点)は存在しないが,並進によって等価な点に移動するので,実質的な不動点とみなせる場合を考えます.このような図形に対しては,並進軸が特異な直線です.図形としては,棒,片面帯,両面帯をとりあげましょう.
1つの点●A1と並進ベクトル➡aが与えられたら,図のように,A1と同価な点がaの間隔で一列に無限に並んでいる点系が得られます.この並進軸は特異な直線と一致しています.
次の図は,平行でない並進軸が2本ある図形で,並進ベクトルbにより1列に並んだ(1次元の)点系がbの方向に次々と繰り返し並び2次元の配列が得られます.3次元への拡張も同様で,平面上に乗らない3つの並進ベクトルで点を配置した無限数の点よりなる系です.点の形の対称性は∞です(点は位置だけを示し形や大きさは意味はありません).1つの点を並進で広げたものなのですべての点は同価です.
格子点は$$na+mb$$,($$a$$,$$b$$を生成元とする加法群の要素)
■第4回:群の表現と性質の対称性(2018.03.27)
色々な電子デバイスは,結晶という舞台で起こる電子や光子のパフォーマンスを利用しています.結晶という舞台で観測される性質の対称性には,それが起こる舞台(=結晶)の対称性が反映されているはずです.これは,Pierre Curieの原理(1894)と呼ばれる因果律です.つまり,性質の対称性(点群)をGp,結晶の対称性(点群)をGcrystとすると,Gp⊃Gcrystであります.分子の形(点群)がわかっているとき,その分子振動モードや,分子軌道のエネルギ-準位の縮退の様子を群論を使って知ることができます.その他,ルビーの赤い色は,コランダム結晶構造のAl原子(その位置は,O原子が囲む正8面体場の中心)を,d電子を持つCr原子(Al原子にはd電子はない)が置き換えたとき,正8面体場の中の置かれたd電子軌道の縮退が解け,緑~青(赤の補色)の光の吸収が起こるためです.
このような性質の対称性の解析には,その舞台の対称性を表現する(群の行列表現)手法が必要になります.
◆群の行列表現
有限群の各元に,複素数を成分とする正則行列を対応(準同型写像)させ,群の演算構造を行列の集合の中に再現することを,群の行列表現と言います.f次元行列表現を得るには,互いに1次独立なf個の基底関数が必要です.群の対称操作を基底関数に作用させると,f個の基底関数の線形結合に変換されますが,このときの変換行列が対称操作の表現行列です.このようにして,群の各元を行列で表現すると,固有値・固有関数などの行列の理論が使えるようになります.
任意のn次複素正方行列Aは,適当なn次のユニタリー行列Pによる相似変換P-1APで,固有値が対角上に並んだ上三角行列に変形できます.互いに相似変換にある行列の固有値は同一です.
相似変換で結ばれる表現行列は同値とするので,有限群Gを共役類に類別すると,同じ共役類に属する対称操作の行列表現は同値(相似変換で結ばれている)なので,表現行列を共役類ごとに得ることができます.
◆表現行列の簡約
分子の形(点群)が与えられたとき,分子の振動モードを調べるには,3N次元の変位ベクトル(Nは分子を構成する原子数)を基底にとります.8面体場中のd電子のエネルギー準位の縮退を調べるには,5つあるd電子軌道の波動関数を基底にとります.選んだ基底関数に対して点群要素の行列表現を作ります.得られた行列表現は,一般には可約であり,適当な相似変換により,対角化あるいは対角ブロック化(各ブロックは既約表現)ができます.これを表現行列の簡約といいます.相似変換は,物理的には基底変換で,適当な基底変換で作った新しい基底に対し,群のすべての対称要素の表現行列が,一斉に対角ブロック化します.
固有値に縮退がなければ,1次元の既約表現が並ぶ対角化ですが,縮退があれば,ブロック細胞(2次元以上の既約表現)が現れます.
基底変換して得た新しい基底は,対角化あるいはブロック対角化に対する固有関数であり,ブロック細胞(既約表現の次元数だけ縮退)を張るものごとに分類されました.
(注)表現行列が既約であるとは,いかなる相似変換をしても対角化できないものです.
表現の簡約は,実際には表現行列の対角和である指標を用いて簡単に計算できます.
群の元の表現行列は群の位数だけありますが,同じ類に属する元の表現行列は同値ですから,類の数だけ表現行列があるとも言えます.したがって,表現行列の指標を並べると,類の数だけの次元を持つベクトルの様なものです.
異なる既約表現の指標は直交するので,これを用いると,与えられた表現行列の中に,既約表現がそれぞれ何個含まれるかを,指標の計算だけで容易に知ることができます.
ルビーの例「正8面体場に置かれたd電子」に戻ると,5つのd電子軌道関数を基底にした5次元の表現行列を簡約し,2次元の既約表現Egと3次元の既約表現T2gの対角ブロックが得られます.自由な場では,5重に縮退していたd電子が,8面体場では,2重縮退と3重縮退の2つのエネルギー準位に分離し,このエネルギー準位間の状態遷移で光の吸収が起こることが説明されました.
■第3回:結晶空間群(2017.12.12)
このシリーズのメインテーマです.結晶空間群Φは,並進群Tを点群Gで拡大して得られます.
逆の言い方をすると,並進群Tは空間群Φの中で正規部分群なので,Tを核とする準同型写像で,空間群Φは点群Gに準同型Φ/Γ=G になります.並進群Tと点群Gとによる拡大の仕方は,(1)点群Gも空間群Φの正規部分群である場合には“直積”,(2)点群Gが非正規部分群である場合は“半直積”です.また,(3)以下に述べる拡張した点群Gとの積の場合は“条件積”と呼ばれます.
空間群の中に現れる点群Gは純粋な点群だけでなく拡張できます.点群Gの中の位数nの演算gはn回繰り返すと gn=1ですが,空間群の中では格子分だけ移動しも同値ですから,(gα)n=1(modT)と拡張できます.つまり拡張された点群には,”映進”や ”らせん軸(3次元の場合)”演算があります.演算gαを含む拡張された点群Gで拡大して得た空間群はnon-symmorphic非共型,純粋な点群Gで拡大して得た空間群はsymmorphic共型と言います.3次元の結晶空間群230種のうち157種,2次元の壁紙模様17種のうち4種がnon-symmorphicです.
◆平面群の作り方(図)
点群G=2mmと,単純長方形格子T=orthoPから,平面群P2mm.P2gm,P2ggの3つが生じます.
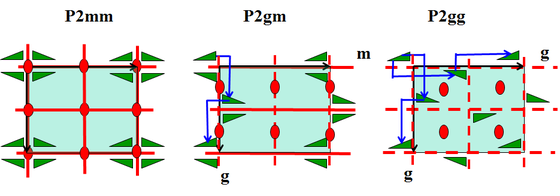
映進gは2回続けると1格子分の移動になるg2=1(modT)ので,格子点はすべて同値という見方をすると平面群 P2mm,P2gm,P2ggは,点群2mmに準同型に還元されます.
■第2回:結晶点群(2017.09.26)
有限図形の対称性は,1点を不動にするような対称操作の組み合わせが作る点群で記述します.私たちの興味は周期的空間(結晶空間)ですから,周期性と両立する対称操作が作る点群は,“結晶点群”に限定されます.2次元結晶空間で許される対称操作は,(位数2)鏡映m,2回軸2:(位数3)3回軸:(位数4)4回軸:(位数6)6回軸だけです.
(注)対称心は3次元以上で存在.5回軸は2次元,3次元では周期性と両立しません.
結晶点群は,2次元では10種類,3次元では32種類,4次元では227種類あります.
3次元の正多面体,半正多面体の対称性を鑑賞し,点群の表記法の例を学びました.
互いに双対な多面体の対称性は同じ.切頂などで正多面体から導いた半正多面体でも対称性は変わりません.結晶格子とその逆格子は,互いに双対で,結晶格子空間に作られるデリクレ胞と,その逆格子空間に作られるデリクレ胞(第1ブリルアン帯)は,互いに双対な多面体になります.
対称性の高・低に関しては,各点群に属する部分群の系列を示しました.群の拡大で必要となる,正規部分群,剰余類展開などを,結晶点群を題材にして具体的に説明しました.直積や半直積による点群の分解は,特に重要な項目です.
万華鏡の対称性は,鏡映のみを生成元として生まれる群ですが,群を生成できる万華鏡の3枚鏡の組み合わせは3通りで.これらの鏡の組み合わせでは,不動点は存在しないので,並進を伴い壁紙模様ができます.
■第1回:周期的空間(2017.06.28)
無限に広がる平面が,1枚のタイル(平行4辺形)を敷き詰めてタイル張りされている状態を考えましょう.辺と辺,頂点を合わせたタイル張りです.
この平面は,タイルを単位胞としてデジタル化された平面といえます.平面のデジタル化により,連続・等方的であった平面に,周期と異方性が生じています.周期的なデジタル空間は結晶空間と呼ばれます.
平行4辺形タイルの2辺は,周期的な2次元世界を張る基本並進ベクトル で,これらの整数係数の線形結合 も並進ベクトルです.並進ベクトルの集合全体のイメージは格子(すべての格子点は同値)です.
(注)2次元だから,互いに独立なベクトルは2本あります.平行6辺形でも平面のタイル張りができますが,対向する2辺間の移動ベクトル3種のうち,互いに独立なものは2つのみです.
対象とする単位胞タイルは,平行移動(並進)だけでタイル張りができるものです.従って,3角形や5角形のタイルは使えません.また,ペンローズのタイル張りのような非周期のタイル張りも対象にしません.
並進ベクトルの集合は,加法で群をなし,これを並進群(無限群)Tと呼びます.
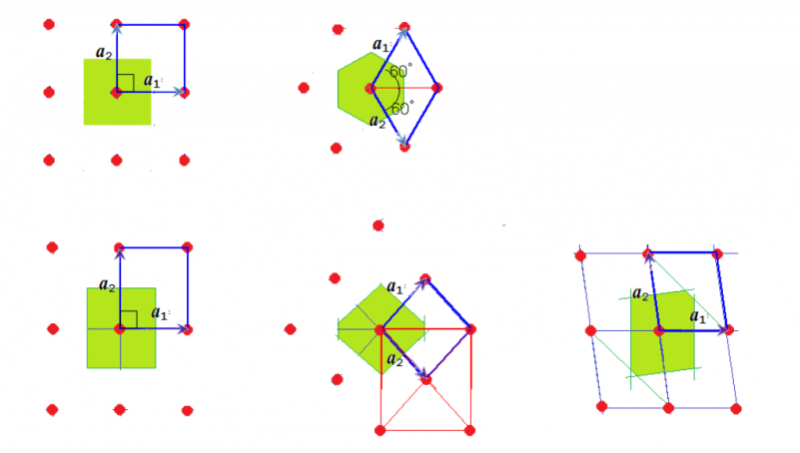
並進群を対称性で分類したものがブラベー格子で,2次元では5種類,3次元では14種類,4次元では74種類のブラベー格子があります.
ブラベー格子を直観的に理解するには,デリクレ(ウイグナー=ザイツ)胞を示すのが良いようです.デリクレ胞とは,1つの格子点に注目し,その格子点と周囲の隣接する格子点を結び,その垂直2等分面で囲んだ胞(あるいは,タイル)です.デリクレ胞は,内部に格子点を1つだけ含み,胞の形の対称性が,このデリクレ胞で張り詰められた無限に続く空間の対称性と同じであることは,自明でしょう.
紙面制限のため,2次元の話にとどめましたが,3次元,さらに高次元の空間でも同様です.この節を終わるにあたり,私の作ったエッシャー様モチーフ「ハロウイン魔女」を鑑賞ください.