河野俊丈(明治大学)
このテーマは,Kavli IPMUにおける数学と宇宙物理の協働研究に関わる.
ガリレイ変換に従う古典力学では,すべての慣性座標系で一つの絶対時間が支配するので,光速は座標系の移動速度の影響を受ける.一方,ローレンツ変換に従う特殊相対論では,どの座標系でも光速は不変(実験事実)としたので,時間は個々の座標系で異なる固有時間$${t'=t\sqrt{1-(v/c)^{2 } } }$$となる.座標系の移動速度$${v}$$が光速$${c}$$に近づくと,その座標系での時間の流れは遅れ,逆に,$${v \ll c}$$ではガリレイ変換の結果$${t'=t}$$に一致することがわかる.
ローレンツ変換に従う真空時空では,計量$${ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2 } }$$が保存されるが,
質量エネルギー分布があるために生じる空間の歪(曲率)は,アインシュタイン重力場方程式により記述されるが,特に,太陽のような天体が作る球対称の重力場に対しては,シュバルツシルト計量が保存される.この時空の光線は,シュバルツシルト計量を保存し,時間が最小となる経路(フェルマーの原理)を進むので,光線経路の偏角を容易に知ることができる.
アインシュタインリング(NASA)
大きな重力場を有する天体の傍らを通過する光線は,その重力場が空間を歪ませているため,時間が最小となる経路をとると曲がっている.重力レンズとは,重力場が示すこの効果を言う.大きな重力場のある天体の輪郭にリング状の光(アインシュタイン・リング)が観測されたり,実際に存在するのは1つのクエーサー(準恒星)であるのに,これが複数個に観測されたり,像が歪むなどの現象が起こる.これらの現象は,身近な光学現象で見られる光線の集まる火面(コスティック;caustic)の形成と同じである.1点の光源から発した球面波の波面は,途中にグラスなどがあると,その表面で反射や屈折を起こし,折り返され方位を変えた複数の球面波の波面になり,波面が重なり光線の集中する火面が形成される.同様な現象が,重力場でも起こり,波面が折り返され重なり,歪んだ光線の集まる火面の像が観測される.
遠方宇宙にあるクエーサーや銀河からの光が,途中で巨大な重力場を通り,観測者Oに達するのだが,像は観測天球面T上にあり,光源は遠方宇宙の天球面S上にある.観測者O,観測天球面Tの点,遠方宇宙の天球面Sの点の3点は,重力場による曲率のある世界の測地線上にある.光線は途中の重力場で曲がるために,実際に光源となったクエーサーや銀河が存在するのは,観測像の延長上ではない.
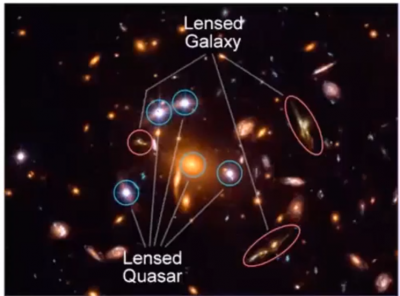
クエーサー,および銀河の像(NASA)
我々が観測するこのクエーサーの像は,火面が引きちぎられて5つに見えるものだが,これらが同一光源からの像であることの証拠は,それらのスペクトルが同一であることによる.なぜ5つに引きちぎられて見えるのかというのは,特異点理論が関わる.2つの天球面間に,なめらかな写像T→Sを考えよう.火面形成に関与する波面の集合は写像の臨界点集合で,カタストロフィー理論(ルネ・トム他)によると,写像の特異点の型は①折り目(fold),②カスプ(尖った点;casp)の型があり,臨界点集合の折り目の外側では写像によってSの1点に写されるTの点の個数は1個であるが,臨界点集合をよぎるたびに2ずつ増加するので,一般には上のようなTの点の個数は奇数となる.この写真のクエーサー像と銀河像は,それぞれ,5個および3個の像に観測されている.
特異点理論は,宇宙観測データの膨大な解析と協働して,宇宙の重力場やダークマター,ブラックホールの分布を知ることにもつながる.