小谷善行(パズル懇話会会長)
パズルはどの様にして作られていくのでしょうか.パズルがクイズと異なるのは知識なしで考えれば解けることです.パズルのタイプには,論理,図形,計算,物体などがあります.パズルがひらめくと,解答の候補を作りその評価を行います.無解や別解があるか検討し,解がただ一つになるように修正します.
図1は自己参照パズルの例です.4か所に当てはまる数を考えてください.実行すると自分自身を印刷するステートメントや,自分が複製,あるいは自己増殖するステートメントのパズルもこの仲間です.
次も論理パズルの例:
男子20人と女子20人のクラスです.最初の女子が「男子のうち少なくとも1人は嘘つきがいる」と言いました.2番目の女子が「男子のうち少なくとも2人は嘘つきがいる」といい,このように次々に進み,19番目の女子は「男子のうち少なくとも19人は嘘つきがいる」と言い,最後の女子は「男子は全員嘘つき」と言いました.このクラスの嘘つきの生徒数は何人かと問います.ーーーーー答えは「20人」です.この論理はたいへん面白い.
パリティ(偶奇性)の支配する世界で,配置が不可能なことを証明する問題があります.10×10の升目の世界に,I型テトラミノの敷き詰めが不可能な証明はパリティ利用で行うことができます.
交差点で必ず曲がる散歩のパズルでも,碁盤の目道路のパリティを利用し解くことが示されました.
物体パズルでは,シリンダー錠の設計に似た「星の姿パズル」などが種々の物が紹介されました.
形のパズルの例では,図2の図形を,同じ形に2分割する方法を問います.
なかなか難しい.お考え下さい.この解はただ1つだそうです.
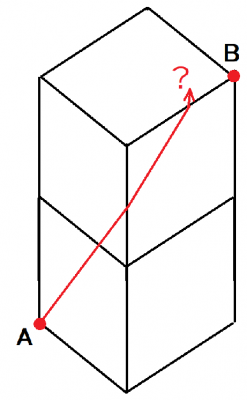
小谷のアリと呼ばれるパズルは,4角柱(立方体を2つ重ねた形)の1つの頂点Aからスタートし,表面を這う蟻の行路で最も遠い位置は何処かを問います(2点間の距離は表面を通り最短なもの.輪ゴムを張ったりして確認できます).答えは体対角線の頂点Bではありません.
ルジンの問題とは,異なる大きさの正方形を敷き詰めて正方形を作るものですが,これが電気回路のキルヒホッフの定理と等価であるとはたいへん興味深い.
他にも多くのオリジナルパズルと,その性質を決めている数学概念について解説がなされました.
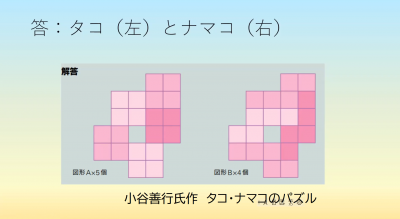
この形の盤の上に,タコは5つ,ナマコは4つ敷詰めることができます.