色付対称の結晶点群
-古典結晶群を色置換群$$P$$および$$G^{(p)*}$$により拡大したもの-
結晶群の新しい拡大類は,何らかの超幾何学的性質の置換群を用いて得られる.この超幾何学的性質(性質数$$p$$は2以上)は,結晶空間の点に付与されたものである.もし,結晶空間のそれぞれの点に,2つの符号(《+》,《―》)だけをとる何らかの演算子$$H$$が結び付けられているなら,性質数は$$p=2$$であり,反対称空間を扱うことになる.そこでは,次の結合された演算が作用している.
$$g'=g1'=1'g$$
ここで,$$g$$は古典的結晶演算$$g \in G$$,$$1'$$は反恒等演算で,点を固定し演算子の符号を変える.演算子$$H$$は,前にも述べたように,磁気運動量,電荷などへの演算子と解釈できる(簡潔に述べると,各点で,ベクトル$$H$$,電荷$$q$$などが定義され,これらの量は,ただ2つの符号《+》,《―》だけをとれる).点に付与された性質数$$p$$が2より大;例えば,$$p=3,4,6,8,12,16,24,48$$としよう(後で,これらの数字を選んだ訳を説明する).もし,$$p=3$$とすると,各点での演算子$$H$$は,3つの異なった値をとることができる.これらを次のように記す.
$$H, \varepsilon H, \varepsilon ^{2}H$$
値$$H$$から,$$\varepsilon H$$に変えるには,$$H$$に絶対値1の複素位相因子$$\varepsilon $$を乗じる.
$$\varepsilon =\sqrt[3]{1}$$ であるから,数$$\varepsilon $$ の通常の積則により巡回群 が定義できる:
$$\varepsilon =\sqrt[3]{1},\varepsilon ^{2}=\left( \sqrt[3]{1} \right) ^{2},\varepsilon ^{3}=\left( \sqrt[3]{1} \right) ^{3}=1$$
($$\varepsilon $$の高次の冪は,この3つのどれかになる)
さらに,結合された演算を定義する.
$$g^{(\varepsilon )}=g\varepsilon =\varepsilon g$$
このとき,演算$$g \in G$$ は3次元空間中の《物質》点の直交変換(点に付与されたすべての性質は,作用後の新しい空間配置でも保存される)であり,演算$$\varepsilon $$ は,単に演算子$$H$$にだけ作用し,固定された点において,その値を変えるだけである.結合された演算の積則は直積を用いて定義できる.
$$g_{i}^{(\varepsilon _{i})} \otimes g_{j}^{(\varepsilon _{j})}=g_{i}g_{j}^{(\varepsilon _{i}\varepsilon _{j})}$$, $$g_{i}\varepsilon _{i} \otimes g_{j}e_{j}=g_{i}g_{j}\varepsilon _{i}\varepsilon _{j}$$ (1)
すでに定義した積則を持つ結合された演算の集合が,どのような条件下で,有限位数の群を作るかという問題を研究しよう.定義により,群は演算のあらゆる冪と恒等演算を必ず含むから,有限群になるための必要条件として,演算 の冪の或るものが1になるという条件を課すことができる.
$$\left( g_{i}\varepsilon _{i} \right) ^{m_{i } }$$あるいは,より一般的に,$$g_{i}^{m_{i } }\varepsilon ^{m_{i}/s_{i } }=1 $$
ただし,$$m_{i}$$は整数,$$g_{i}\varepsilon _{i}$$は考察している集合の任意の演算である.(このような性質を持っている最小の整数は,対称要素$$g_{i}$$の位数で決まる.以下では,このような整数であるとする);$$s_{i}$$は$$m_{i}$$の約数:
$$m_{i}/s_{i}=p_{i}$$, $$\varepsilon ^{p_{i } }=1$$
$$\varepsilon =\sqrt[3]{1}$$の場合に,定式化された条件に適うのは,位数3と6$$(g_{i}=3,6, \overline{6}, \overline{3} )$$の結晶演算$$g_{i}$$と演算$$\varepsilon$$の結合である.$$\varepsilon =\sqrt[4]{1}$$の場合には,同様にして許される結晶演算は,$$g_{i}=4, \overline{4}$$であり,$$\varepsilon =\sqrt[6]{1}$$の場合には,$$g_{i}=6, \overline{6} , \overline{3}$$である.今後,結合された演算$$g^{(\varepsilon )}$$は,演算$$\varepsilon $$で生成される巡回群$$\left\{ \varepsilon ,\varepsilon ^{2},\varepsilon ^{3}, \ldots ,\varepsilon ^{p-1},\varepsilon ^{p}=1 \right\} $$の位数$$p$$を括弧に入れて,結晶記号の肩に標示する.我々の条件を満たすものは,9つの一般巡回群を作る9つの一般演算である**:
$$3^{(3)},4^{(4)},\overline{4}^{(4)},6^{(6)},6^{(3)},\overline{6}^{(6)},\overline{6}^{(3)},\overline{3}^{(6)},\overline{3}^{(3)}$$
-------------------------------------------------------------------------------------------------------------------------------------
*この章内では,式番号を(1)から付ける.前章の式を引用するときには,(3.10),(4.10)などと記す.
**演算$$6^{(3) \pm },\overline{6}^{(3) \pm },\overline{3}^{(3) \pm }$$は,法により巡回群を生む:
$$6^{(3) \pm }(\textrm{mod} 2)=\left\{ 1,6^{(3) \pm },\left( 6^{(3) \pm } \right) ^{2} \right\} $$,
$$\overline{6}^{(3) \pm }\left( \textrm{mod} m \right) =\left\{ 1,\overline{6}^{(3) \pm },(\overline{6}^{(3) \pm })^{2} \right\} $$,
$$\overline{3}^{(3) \pm }(\textrm{mod} \overline{1})=\left\{ 1,\overline{3}^{(3) \pm },\left( \overline{3}^{(3) \pm } \right) ^{2} \right\} $$
-------------------------------------------------------------------------------------------------------------------------------------
もし,演算$$g^{(\varepsilon )}=g\varepsilon =\varepsilon g$$の代わりに,次の演算
$$g^{(\varepsilon ^{p-1})}=g\varepsilon ^{p-1}=\varepsilon ^{p-1}g$$ $$\left( \varepsilon \varepsilon ^{p-1}=\varepsilon ^{p}=1 \right) $$
を定義する.例えば,$$\varepsilon$$の代わりに$$\varepsilon ^{2}$$($$\varepsilon ^{3}=1$$ )をとるなら,9つの一般巡回群(既出の群と同型だが,$$\varepsilon$$の群とは巡回順のみ逆転している)が得られる.
$$\left\{ \varepsilon , \varepsilon ^{2}, \varepsilon ^{3}, \ldots , \varepsilon ^{p}=1 \right\}$$ $$\leftrightarrow$$ $$\left\{ \varepsilon ^{p-1}, \varepsilon ^{p-2}, \varepsilon ^{p-3}, \ldots , \varepsilon ^{0}=1 \right\} $$
$$\varepsilon$$の巡回方向に対応し,順方向あるいは逆方向の一般化群を,右あるいは左($$\varepsilon $$に関し)のように区別し,$$G^{(p)+}$$ あるいは$$G^{(p)-}$$と標記する.例えば,
$$3^{(3) \pm }, 4^{(4) \pm }, \overline{4}^{(4) \pm }, 6^{(6) \pm }, 6^{(3) \pm }, \overline{6}^{(6) \pm }, \overline{6}^{(3) \pm }, \overline{3}^{(6) \pm }, \overline{3}^{(3) \pm }$$
ここで,右の群には《+》,左には《-》が対応している.
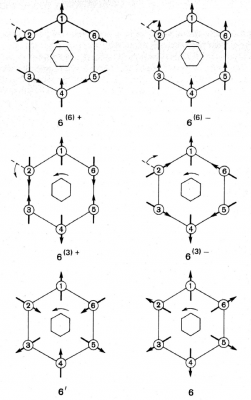
図212ーーーーーーーーーーーーーーーーーーーーーーーーーーーー
色付き点群$$ 6^{(6)+}, 6^{(6)-}, 6^{(3)+}, 6{(3)-} $$,および,反対称群$$6'$$,結晶群$$6$$がもつ磁気配置.これらは,磁気モーメントベクトルに結合された,あるいは,古典的な演算を作用させて得らたもので,すべての配置図で,点1の矢の向きは同一とした.色付き群の標記はまだ標準化されていないので,巡回色付き群の別の記法もある.理論的解析では一般化された群を$$G_{r, t, \cdots, r}^{l, p}$$と記すのが便利である.上の添え字の最初$$l$$は,独立な非幾何学的な座標の数,第2の数$$p$$は群の色数である.この記号では,図の群は,$$G_{3,0}^{1,6}, G_{3,0}^{1,3}, G_{3,0}^{1,2}, G_{3,0}$$(p.198,232,269を参照)
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
図212に示すのは,一般化された群 $$6^{(6)+}, 6^{(6)-}, 6^{(3)+}, 6^{(3)-}$$の磁気的解釈例であり,これらの群を反対称群$$6'$$や古典結晶群$$6$$と比較している.
簡単のために,平面的スピン配位だけを考え,紙面上にある磁気ベクトルを極性の矢で示したが,厳密には,磁気ベクトルは軸性であるから,回転矢印を伴う無極性の線分で表示すべきであることを心に留め置てほしい.
スピンの配位を決めるために,磁気運動量が垂直に向いている番号1の点を出発点とする.回転の正の向きとして,反時計回りをとる.群$$6^{(6)+}$$ における幾何学的な変換$$g$$により,点1から点2へ移動するが,このとき点に固着している磁気モーメントも向きを変え点2においては,半径外向となるであろう.今度は,点2の位置を変えないで,ベクトルにこのベクトルを正の向きに60°回転するような演算子$$\varepsilon $$を作用させると,磁気モーメントは,正六角形を作る向きになる.これが,結合された変換$$6^{(6)+}=\varepsilon 6$$の実行に相当する.この演算を繰り返すことにより,典型的な(非共線の)反強磁性配置ができる.全く同様に,群$$6^{(6)-}$$ に対して,共線の強磁性構造が得られる:反時計回りの回転$$6$$を行い,さらに,これに続けて,ベクトルを時計回りに60°回転する(演算子$$\varepsilon ^{-1}=\varepsilon ^{5}$$を時計回りの60°回転$$6^{-1}$$に結合することは,意味がない,なぜなら,これは,再び$$6^{(6)+}$$ の配置を与えることになる).群$$6^{(3)+}$$ に対しては,反強磁性の共線構造が得られる.他の残りの群$$6^{(3)-},6',6$$は,やはり反強磁性であるが,もはや共線構造ではない.
図212の6つの磁性群は全部互いに異なっている.このように,古典対称および反対称は,結晶における可能な磁気構造としては不十分であり,対称の新しい概念が有用であることが明らかになった.
我々の物質空間の点に,磁気モーメントの演算子を置く代わりに,他の物理特性を置き,それに作用する演算子$$\varepsilon $$を定義することもできる.それぞれの場合につき,得られた一般化された対称群に,新しい具体的解釈を見出すであろう.しかし,得られた群は,既知の一般化された群に同型である.このために,あらゆる場合にあてはまる一般化された群の抽象特性を用いることは有用である.このような抽象特性には,色を選ぶ.空間の点に,色(位相)特性を付与し,演算子$$\varepsilon $$を,固定された点で色(位相)を変える演算子と解釈しよう.
巡回群$$\left\{ \varepsilon ,\varepsilon ^{2},\varepsilon ^{3}, \ldots ,\varepsilon ^{p-1},\varepsilon ^{p} \right\} $$ に対して,自然スペクトル順に色を変えると約束する.例えば,$$6^{(6)+}$$ においては,点1を赤で《塗れば》点2,3,4,5,6はスペクトルの色サイクルを6分割して橙,黄,緑,青,紫と順次塗らなければならない.群 $$6^{(6)+}$$は,このように,《6色の》群で,群$$6^{(3)+}$$ は《3色の》群である.一般に巡回群$$G^{(p)}$$は,$$\varepsilon ^{p}=1$$なら,$$p$$色の群となるであろう.
上で定義した巡回色付き群の他に,巡回ないし非巡回の色置換群も存在する.このような一般化された群全てが,既に述べた18個の群(右-,左-の総計)により,対称,反対称,色付き対称群
$$2,m,\overline{1},4,\overline{4};1',2',m',\overline{1},4',\overline{4};1^{(p)},2^{(p)},m^{(p)},\overline{1}^{(p)},4^{(p)},\overline{4}^{(p)}$$ を拡大して得られる.これは,結晶群を回転群の拡大によって得た(表14)のと全く同様である[訳注:回転群を $$\overline{1},m$$で拡大した].この可能性は読者にまかせ,ここでは,節の冒頭に記した手段によることにする.
色置換群の位数を結晶位数に制限する:$$p=3, 4, 6, 8, 12, 16, 24, 48$$.そして,色付き群$$G^{(p)}$$の中で,上位の結晶部分群$$G^{ \ast }$$が正規商,すなわち,有限指数$$j=p$$の正規部分群を作っているような色付き群$$G^{(p)}$$だけを考える.
$$G^{(p)}=G^{ \ast }g_{1}^{(p_{1})} \cup G^{ \ast }g_{2}^{(p_{2})} \cup \cdots \cup G^{ \ast }g_{j}^{(p_{j})}$$;
$$g_{1}^{(p_{1})}=1, g_{2}^{(p_{2})}, \ldots ,g_{j}^{(p_{j})} \notin G^{ \ast }$$, $$g_{2}^{(p_{2})}, \ldots ,g_{j}^{(p_{j})} \in G^{(p)}$$
数字$$1,2,3, \ldots ,p$$で色特性を表現し,色置換を次のように記す.
$$ p_{j}=\left( \begin{array}{@{\,} ccccc @{\, } } 1 & 2 & 3 & \ldots & p \\[0mm] m_{1_{j } } & m_{2_{j } } & m_{3_{j } } & \ldots & m_{p_{j } } \end{array} \right) $$
下の行には,変換$$p_{j}$$を行ったときに,上の行の番号$$i$$の所がもつ色の番号$$m_{i}$$が書かれている.色置換群は,記号$$p=\left\{ p_{1},p_{2}, \ldots p_{j} \right\} $$で示し,一般化された群$$G^{(p)}$$の結合された演算$$g^{(p)}$$は,交換関係により定義する.
$$g^{(p)}=gp=pg$$
(巡回群の場合には,$$p$$は$$\varepsilon $$に一致する) 結合された演算の積則を定義しよう:
$$g^{(p_{i})}_{i} \otimes g_{j}^{(p_{j})}=g_{i}g_{j}^{(p_{i}p_{j})}$$ あるいは,$$g_{i}p_{i} \otimes g_{j}p_{j}=g_{i}g_{j}p_{i}p_{j}$$ (2)
$$g_{i}, g_{j} \in G, p_{i}, p_{j} \in P, g_{1}=1$$, $$ p_{1}=\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & \ldots & n \\[0mm] 1 & 2 & \ldots & n \end{array} \right) $$
定義に従い,色群$$G^{(p)}$$を古典群$$G^{ \ast }$$の色置換群$$P$$あるいは生成*色付き群$$G^{(p) \ast }$$による拡大と呼ぶ.但し,商群 $$G^{(p)}/G^{ \ast }$$(剰余類$$G^{ \ast }p_{i}$$あるいは$$G^{ \ast }g^{(p_{i})}$$からなる)は,積則$$G^{ \ast }p_{i} \cdot G^{ \ast }p_{j}=G^{ \ast }p_{i}p_{j}$$ あるいは,$$G^{ \ast }g_{i}^{(p_{i})}G^{ \ast }g_{j}^{(p_{j})}=G^{ \ast }g_{i}^{(p_{i})}g_{j}^{(p_{j})}$$ をもち,$$P$$あるいは$$G^{(p) \ast }$$に同型とする.
$$G^{(p)}/G^{ \ast } \leftrightarrow P$$ あるいは $$G^{(p) \ast }\left( P=\left\{ p_{i} \right\} , G^{(p)}=\left\{ g_{i}p_{i} \right\} , g_{i}p_{i} \neq 1^{(p)} \right) $$.
一般化された群$$G^{(p)}$$は,群$$G^{ \ast }$$の色恒等群$$1^{(p)}$$による拡大で得られたものなら,色に関して中性(あるいは混合)と呼ばれる.$$1^{(p)}$$は,$$p$$次のすべての可能な置換からなる位数$$p!=1 \cdot 2 \cdot 3 \cdot \ldots \cdot p$$の対称群$$S_{p}$$として決定される.例えば,$$p=3$$とすれば:
$$ 1^{(3)}=\left\{ \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 1 & 2 & 3 \end{array} \right), \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 1 & 3 & 2 \end{array} \right), \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 2 & 3 & 1 \end{array} \right), \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 2 & 1 & 3 \end{array} \right), \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 3 & 1 & 2 \end{array} \right), \left( \begin{array}{@{\,} ccc @{\, } } 1 & 2 & 3 \\[0mm] 3 & 2 & 1 \end{array} \right) \right\} $$
--------------ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
*生成される群では,色の数は群の位数$$p^{ \ast }=3,4,6,8,12,16,24,48$$に等しい.この基礎に立ち,$$6^{(3) \pm }(\textrm{mod} 2)=\left\{ 1,6^{(3) \pm },\left( 6^{(3) \pm } \right) ^{2} \right\} $$のようなモジュラス群を,文脈から誤解を生じなければ,単に$$6^{(3) \pm }$$と標記する.
-------------- ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
《色恒等演算》を作用させると,空間のすべての点で,中括弧内のすべての演算が同時に実行される.
中性群は,32の結晶群$$G$$と色恒等群$$1^{(p)}$$の直積として定義される:
$$G1^{(p)}=G \otimes 1^{(p)}=1^{(p)} \otimes G$$
$$p=3,4,6,8,12,16,24,48$$としたから,
全部で8つの群$$1^{(p)}$$と,$$32 \times 8=256$$の中性群$$G1^{(p)}$$が定義される.
内訳は,$$n$$を生成群の位数としたとき,$$p=n$$のとき28の群,$$p<n$$のとき90,$$p>n$$のとき138となる.特に,中性群は結晶が,どのような位相特性をもつことも許容しない.
例えば,一般化された群の磁気解釈の際に,磁気ベクトルに,群演算$$1^{(p)}$$を適用すると,各点で,合力0のベクトルの星形を得るはずである.これは,群$$G1^{(p)}$$が,結晶に定常的磁気構造を持つことを許容しないということである.
結晶群$$G$$に同型な真の色付き群(非中性)$$G^{(p)}$$は,正規商$$G^{ \ast } \vartriangleleft G$$があり,これと,生成色群$$G^{(p) \ast }$$あるいは,$$6^{(3) \pm }(\textrm{mod}2)$$のようなモジュラス群$$G^{(p) \ast }(\textrm{mod}G_{1}^{ \ast })$$との直積,半直積,あるいは条件積を作り得ることが出来る.★
$$G^{(p)}=G^{ \ast } \otimes G^{(p) \ast }, G^{(p)}=G^{ \ast } \oslash G^{(p) \ast }, G^{(p)}=G^{ \ast } \odot G^{(p) \ast }(\textrm{mod}G_{1}^{ \ast })$$
群 の同型性$$G^{(p)} \leftrightarrow G$$は,部分群$$G^{ \ast } \vartriangleleft G$$の指数$$s$$が,選ばれた生成色群$$G^{(p) \ast }$$あるいは$$G^{(p) \ast }(\textrm{mod}G_{1}^{ \ast })$$の位数$$p^{ \ast }=3,4,6,8,12,24,48$$に一致すれば保証される:
$$G^{ \ast }=G^{(p)} \cap G, G^{(p)}/G^{ \ast } \leftrightarrow G^{(p) \ast }$$または$$G^{(p) \ast }(\textrm{mod}G_{1}^{ \ast })$$
本来の色付き群は,色恒等部分群(color-identification group)$$1^{(p)}$$を含まない $$1^{(p)} \not\subset G^{(p)}$$ことを忘れてはならない.すなわち,色対称群の色置換は,恒等変換ではない幾何学変換と結合されねばならない.
表18には,色群が,直積,半直積,条件積の型で表現されている.これらの記号は,結晶群の国際記号に基づいて作られる:各々の色元$$g_{i}^{(p_{i})}$$ と群全体$$G^{(p)}$$には,色指数$$p_{i}$$と$$p$$が標示される.この記号で,数$$p$$は独立な生成元の色指数$$p_{i}$$の積に等しい;例えば,群$$\left( \displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(8)}$$では,$$p=2 \times 2 \times 2$$となる.なぜなら,この群は3つの生成元から作られているからである.数$$p_{i}$$は色元の位数と一致する:$$\left( g^{(p_{i})} \right) ^{p_{i } }=1$$ .これは,非巡回群$$G^{(p)} (p>p_{i})$$で,元 $$g_{i}^{(p_{i})}$$に付随した$$p$$文字(色)の置換は,長さ$$p_{i}$$の循回置換に分かれることを意味する:
$$ p_{i}=\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & \ldots & p \\[0mm] m_{1} & m_{2} & \ldots & m_{p} \end{array} \right) \left( \begin{array}{@{\,} ccc @{\, } } 1 & \ldots & m_{1} \\[0mm] m_{1} & \ldots & 1 \end{array} \right) \left( \begin{array}{@{\,} ccc @{\, } } 2 & \ldots & m_{2} \\[0mm] m_{2} & \ldots & 2 \end{array} \right) \left( \begin{array}{@{\,} ccc @{\, } } j & \ldots & m_{j} \\[0mm] m_{j} & \ldots & j \end{array} \right) $$,
$$p=p_{i} \times j$$
置換群 において,$$P=\left\{ p_{1}, p_{2}, \ldots , p_{n} \right\} $$,$${p }$$数を長さ$$p_{i}$$項の巡回置換に分けるあらゆる異なった分け方と,色生成元と古典生成元の許容される結合を見出すことは,色対称群$$G^{(p)}$$($$p \le n$$ のとき)導出の出発点となる問題である.もし,結晶群の位数$$p$$を制限しないなら,非結晶色群を得ることが出来る.$$\left( \displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(8)}$$型 の色群を,簡単に,$$\displaystyle \frac{2^{(8) } }{m^{(8) } }\displaystyle \frac{2^{(8) } }{m^{(8) } }\displaystyle \frac{2^{(8) } }{m^{(8) } }$$ と短縮することも出来る.なぜなら,巡回の長さ情報$$p_{i}$$は,結晶元 によって与えられるからである:$$g_{i}^{p_{i } }=1$$
表18で出会うモジュラス群$$G^{(p) \ast }(\textrm{mod}G_{1}^{ \ast })$$は,既に出会った型$$4(\textrm{mod}2)=\left\{ 1,4 \right\} ,4'(\textrm{mod}2)=\left\{ 1,4' \right\} $$等と比べて,特に通常と異なる訳ではない.モジュラス群の使用は,色対称群を単に結晶群の拡大と見なすだけでなく,対応する色群の拡大と見なすなら,避けることが出来る.この場合には
$$ \left( 4^{(2)}2^{(2)}2^{(2)} \right) ^{(4)}=2'2'2 \oslash 2''=4' \oslash 2'' $$,
$$\left( 4^{(2)}/m^{(2)} \right) ^{(2)}=4' \otimes \overline{1}''=4' \otimes m''$$,
$$\left( 4^{(2)}m^{(2)}m^{(2)} \right) ^{(4)}=m'm'2 \oslash m''=4' \oslash m''$$, $$\left( \overline{4}^{(2)}2^{(2)}m^{(2)} \right) ^{(4)}=2'2'2 \oslash m''=\overline{4}' \oslash m''$$,
$$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(8)}=\overline{1}^{(2)} \otimes \left( 4^{(2)}2^{(2)}2^{(2)} \right) ^{(4)}$$,
$$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } }\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(4)}=2'2'2 \oslash \displaystyle \frac{2''}{m''}=2'2'2 \oslash mm''2''$$,
$$\left( 4^{(2)}3^{(2)}2^{(2)} \right) ^{(6)}=2^{(2)} \otimes \left( 23^{(3)} \right) ^{(3)}$$, $$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\overline{3}^{(6)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(12)}=\overline{1}^{(2)} \otimes \left( 4^{(2)}3^{(3)}2^{(2)} \right) ^{(6)}$$,
$$\left( \displaystyle \frac{4^{(2) } }{m}\overline{3}^{(3)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(6)}=\overline{1} \otimes \left( \overline{4}^{(2)}3^{(3)}2^{(2)} \right) ^{(6)}$$
(ただし,$$\overline{1} \subset \displaystyle \frac{2}{m}\displaystyle \frac{2}{m}\displaystyle \frac{2}{m}=G^{ \ast } \subset G^{(p)}$$)
(記号$$'$$と$$''$$で,2色群の独立な演算子(反対称)を区別する:
$$2'=2^{(2)},2''=2^{(2) \ast },m''=m^{(2) \ast },$$など)
図213 a-fに,$$2/m$$と$$m\overline{3}m$$に同型な色群のステレオ投影を,黒白版で導いた.図面には図69に対応する古典部分群$$1(\textrm{a,b}),\overline{1}(\textrm{c}),222(\textrm{d}),\displaystyle \frac{2}{m}\displaystyle \frac{2}{m}\displaystyle \frac{2}{m}(\textrm{e}),23(\textrm{f})$$の対称元を,白色で記入してある.
残りの元は,真の色元,すなわち,これを用い,$$g^{(p)}=gp$$の型の結合された変換を実行できる.ここで,$$g \in G \leftrightarrow G^{(p)}$$ ,$$p$$は色(数字)置換で,演算子の超幾何学的部分の働きで,与えられた点で実行される.
符号$$ \pm $$は,ステレオ投影で,図面上に投影された非対称点(4面体)が,上半球から来たか下半球から来たかの状態表示である.
符号の違う各対$$ \pm $$は,同一の点に投影されたものである.図213$$\textrm{a-f}$$に示された同価系の点には色がある:点の《色》は対応する番号で示される.4色群 $$\left( 2^{(2)}/m^{(2)} \right) ^{(4)}$$は次の結合された演算よりなる:
$$ 1=1\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & 3 & 4 \\[0mm] 1 & 2 & 3 & 4 \end{array} \right) =1(1)(2)(3)(4) $$;
$$ 2^{(2)}=2\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & 3 & 4 \\[0mm] 2 & 1 & 4 & 3 \end{array} \right) =2(12)(34) $$;
$$ m^{(2)}=m\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & 3 & 4 \\[0mm] 3 & 4 & 1 & 2 \end{array} \right) =m(13)(24) $$;
$$ \overline{1}^{(2)}=\overline{1}\left( \begin{array}{@{\,} cccc @{\, } } 1 & 2 & 3 & 4 \\[0mm] 4 & 3 & 2 & 1 \end{array} \right) =\overline{1}\left( 14 \right) (23) $$.
元$$g^{(p)}=gp$$を定義しているこれらの等式の右辺で,置換$$p$$は,完全な形と短縮(巡回置換)形とで書かれている( $$g^{(p)}$$の指数$$(p)$$は,巡回置換の長さに対応している).
演算$$2^{(2)},m^{(2)},\overline{1}^{(2)}$$に対応する色対称元は,異なる色に塗られるべきである.なぜなら,これらにより実現される色(数字)置換は異なるからである.対称群$$\left( \displaystyle \frac{4^{(4) } }{m^{(2) } }\overline{3}^{(6)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(48)}$$のすべての元も異なる色に塗られるべきであることはすぐわかる.
定義から,生成演算の一次で与えられる色対称の元$$g_{i}p_{i}$$と$$g_{j}p_{j}$$は,これらの元が,同一の色置換,すなわち,$$p_{i}=p_{j}$$ならば,同じ色に塗られる.このような場合は,次の群の時に出会う.
$$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\overline{3}^{(3)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(24)}=\overline{1} \otimes \left( 4^{(4)}3^{(3)}2^{(2)} \right) ^{(24)}$$,
$$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\overline{3}^{(6)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(12)}=222 \odot \left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\overline{3}^{(6)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(12)}\left( \textrm{mod}222 \right) $$,
$$\left( \displaystyle \frac{4^{(2) } }{m}\overline{3}^{(3)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(24)}=\displaystyle \frac{2}{m}\displaystyle \frac{2}{m}\displaystyle \frac{2}{m} \odot \left( \displaystyle \frac{4^{(2) } }{m}\overline{3}^{(3)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(6)}\left( \textrm{mod}\displaystyle \frac{2}{m}\displaystyle \frac{2}{m}\displaystyle \frac{2}{m} \right) $$,
$$\left( \displaystyle \frac{4^{(2) } }{m^{(2) } }\overline{3}^{(2)}\displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(4)}=23 \oslash \left( \displaystyle \frac{2^{(2) } }{m^{(2) } } \right) ^{(4)}$$
最後の群では,例えば,すべての対角diagonalの鏡映面$$m$$に置換$$(13)(24)$$が結び付けられている.対称心と座標平面$$m_{x},m_{y},m_{z}$$は,置換$$(14)(24)$$に,軸$$2_{i}$$と$$4_{j}^{(2)}$$は置換$$(12)(34)$$に結び付けられている.この群の表示のためには,黒の他に3色必要である.
図213$$\textrm{a-f }$$にも表18にも,群$$G^{(p)}$$の81の象徴が,色対掌体enantio-と多形polymorphismの区別なしで導かれている;色対掌体enantio-と多形polymorphismの考慮をすると群$$G^{(p) \pm }$$の数は134に増加する.これらのうち37群だけが生成群である:28群は自明な$$G^{(p)}=1 \otimes G^{(p)}$$,9群は$$G^{(p)}(\textrm{mod}G^{ \ast }_{1})$$.色巡回置換による群は,最初にniggli(1959)とIndenbom,Belov,Neronova(1960)により得られた.古典的正規商normal classical divisors нормальные классические делителиを含む群は,Wittke(1962)が研究した.合理的な表現rational symbolism рациональная символиса,ステレオ投影stereographic projections стереографические проекции,色群の積の型への分解表現form of products of cofactors в форме произведений сомпожителейは,我々により,初めてここに導かれた.群$$G^{(p)}_{N}=G^{ \ast }G^{(p) \ast }$$(表18)は,73のWittke-Garrido群$$G^{(p)}_{WG}=G^{(p) \ast } \cdot G^{ \ast }$$および,これらに同型な73の$$\textrm{Van der Waerden-Burckhardt }$$群,$$G_{WB}^{(p)}=G^{(p_{1}) \ast } \cdot G^{(p_{2}) \ast }$$(非自明な正規古典部分群を含まない)で補充できる.既知の群 $$(4^{(2)}m^{(2)}m^{(2)})^{(4)}=4^{(2)} \oslash m^{(2) \ast }$$, $$\left( 4^{(2)}2^{(2)}2^{(2)} \right) ^{(4)}=4^{(2)} \oslash 2^{(2) \ast }$$,$$\left( \overline{4}^{(2)}2^{(2)}m^{(2)} \right) ^{(4)}=\overline{4}^{(2)} \oslash m^{(2) \ast }$$を見本として(参照p.243),新しいWittke-Garrido群を得ることが出来る.例えば;
$$\left( 4^{(4) \pm }mm^{(2)} \right) ^{(4)}=4^{(4)} \oslash m$$,
$$\left( 4^{(4) \pm }22^{(2)} \right) ^{(4)}=4^{(4)} \oslash 2$$,
$$\left( \overline{4}^{(4) \pm }2m^{(2)} \right) ^{(4)}=\overline{4}^{(4)} \oslash 2$$,
$$\left( \overline{4}^{(4) \pm }2^{(2)}m \right) ^{(4)}=\overline{4}^{(4)} \oslash m$$
あるいは,新しいVan der Waerden-Burckhardt群
$$\left( 4^{(4)+}m^{(2)}m^{(2)} \right) ^{(4)}=4^{(4)} \oslash m^{(2)}$$,
$$\left( 4^{(4)+}2^{(2)}2^{(2)} \right) ^{(4)}=4^{(4)} \oslash 2^{(2)}$$,
$$\left( \overline{4}^{(4)+}2^{(2)}m^{(2)} \right) ^{(4)}=\overline{4}^{(4)} \oslash 2^{(2)}$$,
$$\left( \overline{4}^{(4)+}2^{(2)}m^{(2)} \right) ^{(4)}=\overline{4}^{(4)} \oslash m^{(2)}$$
部分群$$G^{(p_{2}) \ast } \subset G^{(p)}_{WG}$$は,最後に決まった色を保存する;群$$G_{WG}^{(p)}$$中の色置換の型$$G^{(p) \ast }$$は,始めの点のとり方に依存する.